Valuable Sites to Visit:

Fractals, Chaos

Chaos, Fractals, Dimensions...

The Non-Linear Lab

Recurrence Plots

Rossler Attractor

Lorenz Attractor

The Lorenz Attractor in 3D

3-D Strange Attractors

Orderliness from Chaos

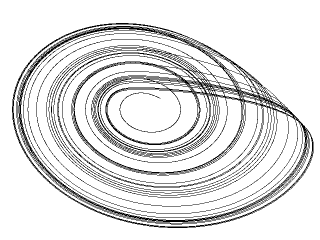
Pictures often provide more information than equations can offer. By graphing points, mathematicians can study the behavior of a mathematical model and the system it models. By graphing the points of non-linear equations, scientists hoped that they could understand the system more full. There were no discernible patterns at first. It appeared that points appeared at random positions and had no relationship to each other. But, using computers, mathematicians were able to create a vast number of points to graph. Eventually, they discovered that the system settled into a pattern. Although no point repeated itself, (affirming that the system was unpredictable) all points stayed within the boundaries of the pattern. In addition, it seemed that the patterns revolved around a central area that appeared to attract the points, like a vortex attracting everything to itself. These images were called strange attractors and were the first images of the order lying within these dynamical systems. The Lorenz Attractor was discovered when Lorenz mapped the points created during his study of meteorological data. It looks like an owl's face with two areas of attraction at the center of each loop (pictured within this text). The black and white graphic used on this page is the Rossler Attractor. To find out more about these, click on those sites.

In addition to graphing points in a 2 dimensional plane, mathematicians began to experiment with images produced in 3 dimensions using complex numbers. This allowed them to study systems that were described using these values. These studies are relatively new. Consequently, we are only just beginning to see the applications for chaos theory. Tom Stilson at Stanford University has a wonderful site on 3-D strange attractors, as well as recommended reading. Click on 3-D Strange Attractors to see what he offers.

Demonstrations:

• Chaos Demonstrations: graphically demonstrates dynamic systems. Need JAVA

Activity:

• Graphing Linear Functions on a Spreadsheet:graph linear functions using Excel and then compare to graphs of non-linear functions.